格子点を2色で塗り分ける問題
先日、Twitterで次のような問題を見かけました。
その日の夜ベッドで考えながら寝たところ、朝起きて5分ほどで思いがけず綺麗に解くことができたので、解法を紹介したいと思います。証明のアイディアは下の記事に取り上げられているVan der Waerdenの定理に似ています。
同色の正方形を作る前に、同色の「L字型」(正方形の右上以外の頂点)を作りましょう。実はこれは何色で塗り分けても存在します。
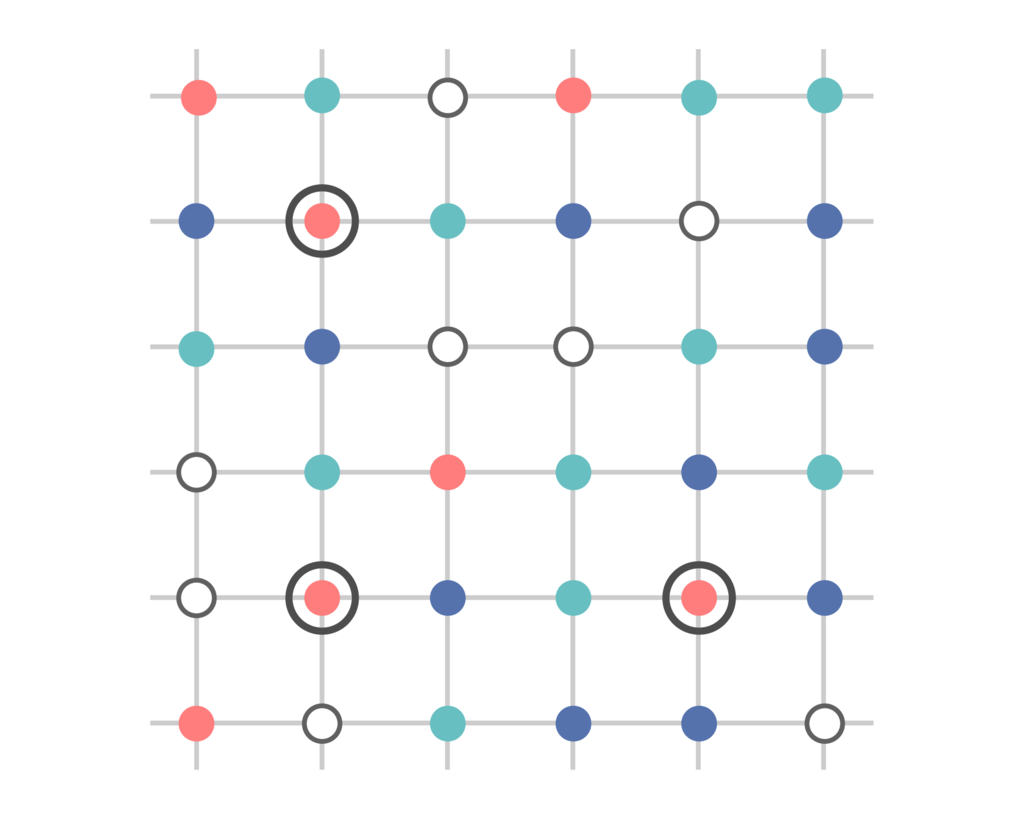
同色のL字型が無いと仮定します。すると実は十分大きい正方形領域をとれば、下図のような「左上の頂点を共有する個のL字型の集まりで、各段の色が異なるもの」を見つけることができるのです。このような点の集まりををわかりやすく「
段のオブジェ」と呼び、左上の頂点をその先端と呼ぶことにしましょう。
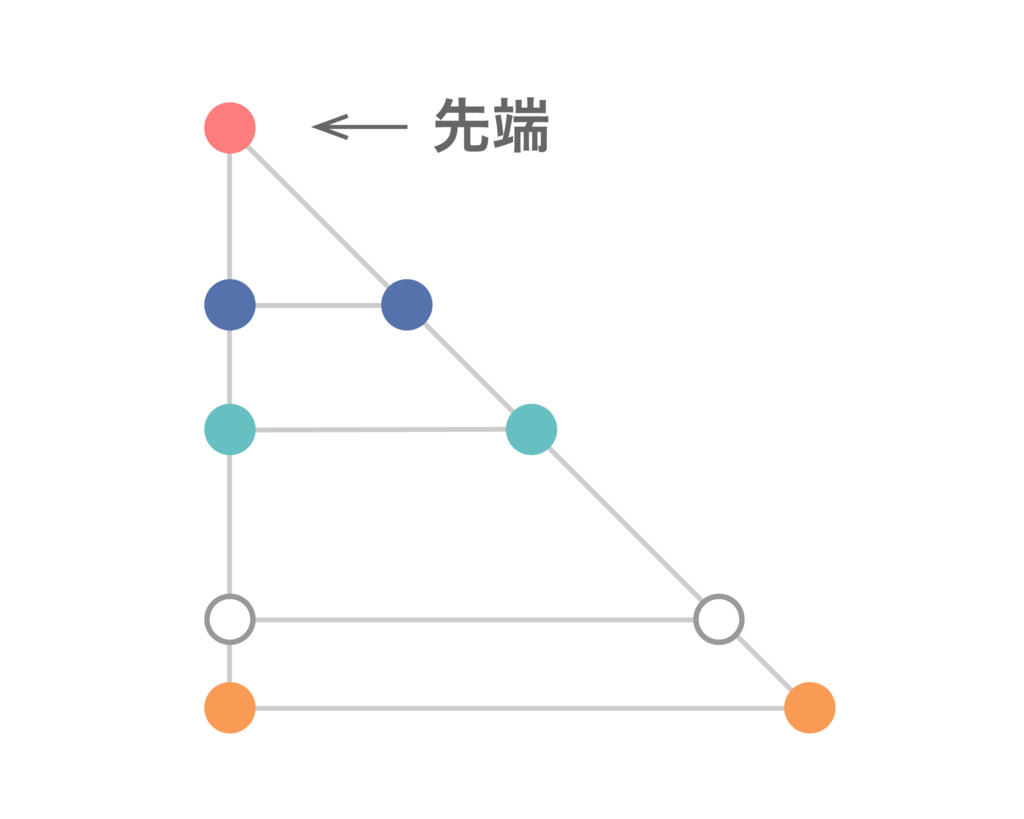
さて、実際に段のオブジェを見つける方法を帰納的に示します。
のときは任意に1点とればそれが
段のオブジェになります。
のとき、帰納法の仮定によりある整数
について
の正方形領域をとれば必ずその中に
段のオブジェが存在します。そこで
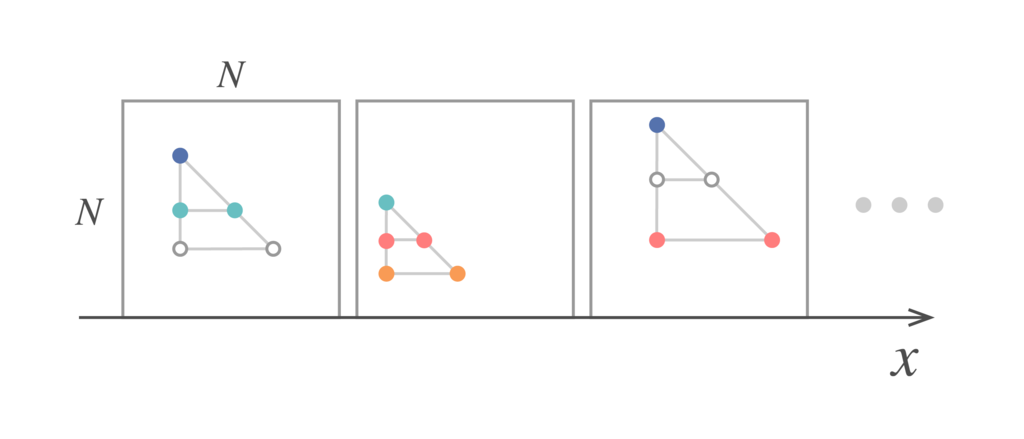
の正方形の列を
軸に平行にとり、それぞれの正方形に含まれる
段のオブジェを1つずつ選びます。そしてこれらの正方形に「選んだオブジェの配色と配置」を記したラベルをつけます。するとラベルの種類は有限なので、同じラベルのついた2つの正方形を取ることができます。
これで同じ配色の段のオブジェが横に2つ並んだ状況ができました。このときオブジェの先端2つとL字型をなす点
をとると、
はオブジェの各段の点ともL字型をなしているので、「同色のL字型が無い」という仮定よりオブジェに含まれるどの色とも異なる色で塗られていなければなりません。よって
と2つのオブジェを合わせれば
段のオブジェができます。

このように任意の段数のオブジェを作ることができるのですが、使う色は有限種類なのでそれより多い段数のオブジェを作ることはできず、矛盾します。これで同色のL字型が存在することが示せました!
2色の場合に戻りましょう。L字型が取れれば、正方形を見つけるのは簡単です。上に書いたことよりある整数について、
の正方形領域には必ず同色のL字型があります。そこで平面を
の正方形たちに分割し、各々に含まれる同色のL字型を1つずつ選んで、その色と配置を記したラベルをつけます。正方形たちを格子点とみなしラベルを色とみなすと、再び上に書いたことより、L字型に並んだ同じラベルの正方形3つを見つけることができます。このとき各正方形内のL字型を集めれば、下図左のように全て同色のL字型がL字型に並んだものが得られます。わかりやすいように、これらL字型の色を青, もう片方の色を赤とします。
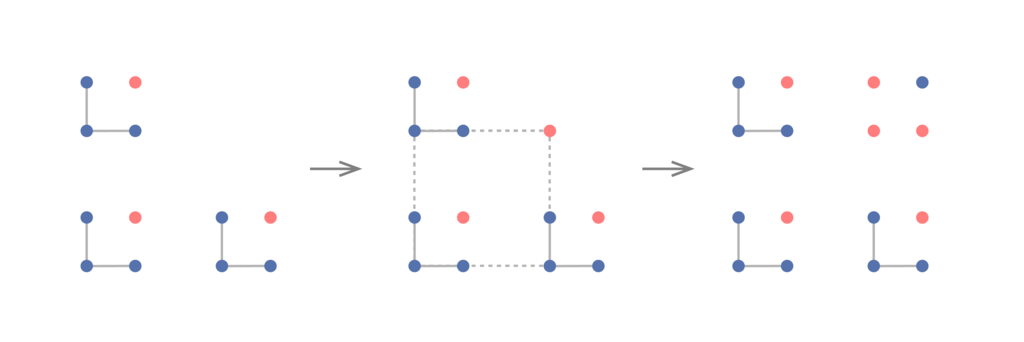
同色の正方形が存在しないとすると、小さいL字型の右上は赤となります(左)。また破線の正方形の右上の頂点も赤でなくてはいけません(中)。同じように右上の4点の色が定まります(右)。このとき一番外側の正方形は全て青で塗られており矛盾します。よって同色の正方形が存在することが示されました。
