HEXの定理(1)
HEXというボードゲームを知っていますか？
1940年代に作られたゲームなのですが、最近はスマホのアプリにもなっているようです。私が高校生の頃はよく同級生が遊んでいました。
HEXは六角形のタイルが敷き詰められたひし形の盤で遊びます。2人で交互にタイルを自分の色（赤か青）で塗り、自陣である向かい合う辺を自分の色のタイルでつないだ方が勝ちとなります。言葉で説明するのは難しいので、下の図を見てください。
図の場合、赤が上下の赤の陣地をつないでいるので赤の勝ちとなります。
ここで自然に湧く疑問があります。
赤も青も勝たないまま全てのタイルが塗られてしまうことはあるのか？
つまり、HEXに引き分けはあるのか？
結論から言うと、HEXに引き分けはありません。このことはHEXの考案者の1人であるNash（ゲーム理論で有名なあのNashです！）自身が証明し、HEXの定理と呼ばれています。
定理. HEXに引き分けは存在しない。すなわち全てのタイルが塗られていれば、どちらかの色は自陣をつないでいる。
証明. 便宜上、盤の外も自陣の色を延長して赤と青で塗られているとする。赤と青の接する境界線を全て描く（下図の白線）。
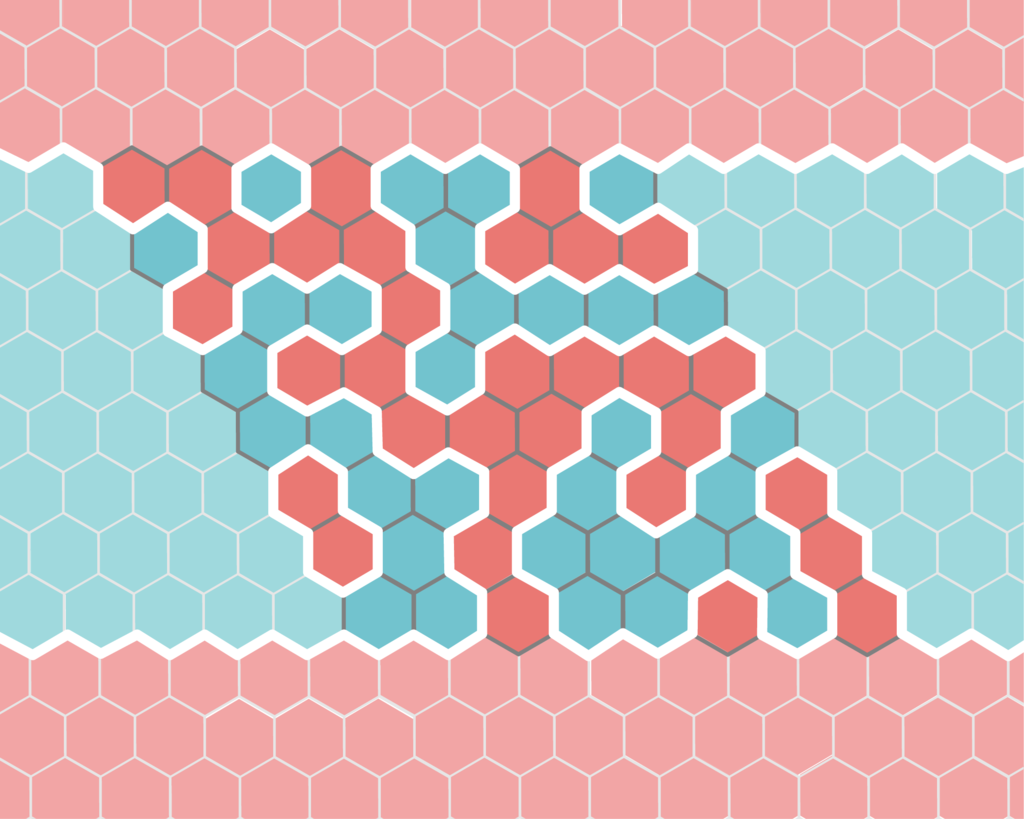
曲がり角の塗られ方を考えれば、この線は途中で切れたり分岐したりしないことがわかる。よって図の左右から出ている4本の境界線は2本ずつ結ばれることになる。すなわち下図のいずれかのようになる。
左の場合は青、右の場合は赤が勝っている。
スマートな証明ですね。
しかしHEXの定理の面白さはその証明だけにとどまりません。なんとHEXの定理は2次元におけるBrouwerの不動点定理と同値なのです！
ここで証明を紹介したいのですが、とても面白い証明なので、まずは是非皆さん自身で考えてみてください（私自身は考える前に証明を読んでしまい少し悔しい思いをしました）。意外と素直に証明できます。ヒントが欲しい方はTwitterなどで連絡してください。
証明は次の「HEXの定理(2)」で紹介します。お楽しみに！
