HEXの定理(2) - フィボナッチ・フリーク

この記事は以下の記事の続きです:

fibonacci-freak.hatenablog.com

さて、前回はHEXの定理とBrouwerの不動点定理が実は同値であるということを紹介しました。今回はその証明を書こうと思います。それぞれのステートメントを確認しておきましょう。

定理(HEXの定理). HEXに引き分けは存在しない。すなわち全てのタイルが塗られていれば、どちらかの色は自陣をつないでいる。

定理(Brouwerの不動点定理). $D=[0,1]^2$ とすると、任意の連続写像 $f:D\to D$ は不動点（ $f(x)=x$ なる点）をもつ。

証明のための第一歩はHEXの定理の次のような言い換えです。

命題. 下図のようなグラフ $G_n$ の頂点を赤と青の2色で塗り分ける。このとき次のいずれかが存在する。
(1)上下の辺を結ぶ道で赤い頂点からなるもの。
(2)左右の辺を結ぶ道で青い頂点からなるもの。

f:id:fibonacci_freak:20170824231208p:plain

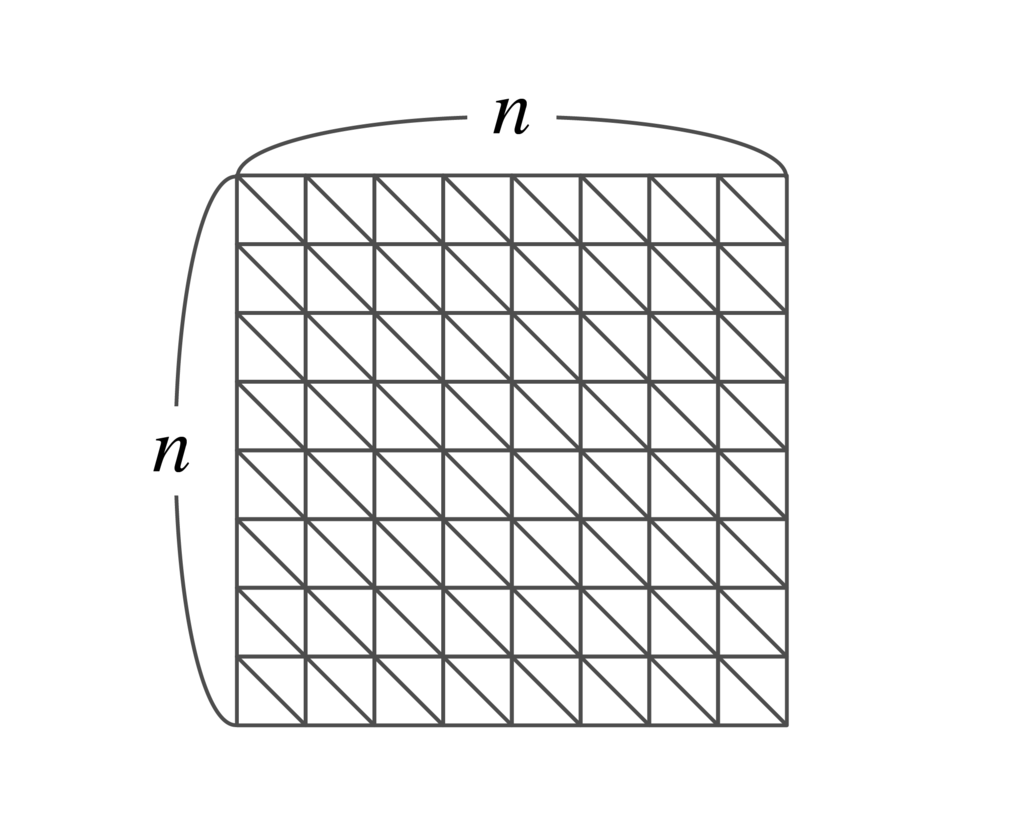
HEXの盤面をそのままグラフに直せば、これがHEXの定理と同値であることがわかります。

それでは不動点定理との同値性を証明しましょう。

HEXの定理 $\Rightarrow$ 不動点定理.

$f:D\to D$ に不動点が存在しないと仮定する。 $|f(x)-x|$ は $D$ 上で最小値を持つのでそれを $\varepsilon\gt0$ とする。また上図のグラフ $G_n$ を、上下左右の辺が $D$ の上下左右の辺上に来るように $D$ 内に配置する。このときグラフ上の任意の点について $f$ による $x$ 座標, $y$ 座標の変化のいずれかは $\varepsilon/2$ 以上なので、前者なら赤に、後者なら青に塗る。両方を満たす場合はどちらに塗ってもよい。上の命題より上下の辺を結ぶ赤い頂点からなる道があるとしても一般性を失わない。

さらにこの道上の頂点を、 $f$ により $y$ 座標が $\varepsilon/2$ 以上減少するならば白、増加するならば黒で塗り分ける。道の上端の点は白、下端の点は黒なので、道中の連続する2点 $A,B$ で色が異なるものが存在する。 $n$ を十分大きくとれば $|A-B|$ は任意に小さくでき、かつ $|f(A)-f(B)|\gt\varepsilon/2$ とできる。これは $f$ の一様連続性に反する。 $~~~\square$

不動点定理 $\Rightarrow$ HEXの定理.

上と同様に $D$ に $G_n$ を埋め込む。命題の(1)(2)いずれも成立しない塗り分けがあったとすると、頂点集合には以下の4つの交わらない部分集合が存在する。

$N=\{$ 上の辺からの赤い道がある赤い頂点 $\}$

$S=\{N$ に属さない赤い頂点 $\}$

$W=\{$ 左の辺からの青い道がある青い頂点 $\}$

$E=\{W$ に属さない青い頂点 $\}$

そして十分小さい $\varepsilon\gt 0$ をとり、 $g:V(G_n)\to D$ （ $V(G)$ は $G$ の頂点集合を表す）を以下のように定める。

$v_1=\dbinom{0}{\varepsilon}, v_2=\dbinom{\varepsilon}{0}$

$g(P)=\begin{cases}P-v_2~~(P\in N)\\P+v_2~~(P\in S)\\P+v_1~~(P\in W)\\P-v_1~~(P\in E)\end{cases}$

ただし仮定から $g$ の像は $D$ に入ることに注意する。

$g$ を小三角形ごとに線形に補間することで連続写像 $f:D\to D$ が得られる。不動点定理より $f$ の不動点 $x$ が存在する。 $x$ を内部に含む $G_n$ の小三角形の頂点 $P_1,P_2,P_3$ を取ると、 $\{f(P_i)-P_i\}$ の凸包は原点を含むので、これらの頂点は $N,S,W,E$ のうち相異なる3つに属する。 $P_1,P_2$ がそれぞれ $N,S$ に属するとしても一般性を失わない。しかし $P_1,P_2$ は辺で結ばれているから $P_2$ は上の辺からの赤い道があることになり $P_2\in S$ に矛盾する。 $~~~\square$

組み合わせ論と位相幾何の間のアナロジーは多々ありますが、このように綺麗に同値になる例は少ないように思います。