2017-08-14

自作数学パズル保管所を開設しました

実は私は最近数学パズルを自作するのにハマっており、時々Twitterなどで出題しています。しかしTwitterではすぐに過去の問題が流れていってしまい、後から見つけるのが大変です。そこで自作パズルを別のブログにまとめておくことにしました。

parabolic-puzzles.hatenadiary.jp

（なぜかhatenablog.comではなくhatenadiary.jpになってしまい悲しいです）

みなさんぜひチャレンジしてください！

2017-08-13

素数の無限性の一風変わった証明

素数組み合わせ論

素数が無限に存在することはもはや人類の常識と言えますが、その証明を沢山知っている人は少ないように感じます。

私は証明そのものを鑑賞するのが好きなタイプなので、以前からずっと素数の無限性のオリジナル証明を作れないかと考えていたのですが、この間ついに組み合わせ論的な証明を思いつきました。組み合わせ論の最も美しい（？）定理の一つ、Van der Waerdenの定理を使う証明です。

定理(Van der Waerden). 正整数全体をどのように有限色で塗り分けても、任意の長さの同色の等差数列が存在する。

この定理の証明は以下の記事などに紹介されています。

integers.hatenablog.com

しかし残念なことに、関連するキーワードで検索したところ、私の考えたものとほぼ同じ証明が既に別の人（L. Alpoge氏）によって発表されていました。しかも私の証明には穴があって、彼の論文ではそれが埋められていることにも気づきました。数学の世界は厳しいですね！

そういうわけで悔しいのですが、せっかくなので今回は彼の証明を紹介したいと思います。今回の記事では正整数 $n$ が素数 $p$ で割れる回数を $v_p(n)$ で表します。

定理. 素数は無限に存在する。

証明. 素数が有限個だったと仮定すると、正整数全体を「素因数に現れる素数の種類とそれぞれの指数の偶奇」を色として塗り分けることができる。どの素数の2乗よりも大きい正整数 $r$ をとると、Van der Waerdenの定理より $a,a+d,\cdots,a+dr$ という同色の等差数列が存在する。このとき $a$ の任意の素因数 $p$ について $p\mid a+d$ だから $p\mid d$ 。

(1) $v_p(a)\gt v_p(d)$ とすると $v_p(a+d)=v_p(d)\lt v_p(a)$ なので、 $a$ と $d$ で $p$ の指数の偶奇が等しいことから $v_p(a)\gt v_p(d)+1$ 。このとき $v_p(a+pd)=v_p(pd)=v_p(d)+1$ となって、 $a+pd$ と $a+d$ が同色であることに矛盾する。

(2) $v_p(a)=v_p(d)$ とすると $a=p^nA$ , $d=p^nD$ （ $A,D$ は $p$ と互いに素）と書ける。 $\mathrm{mod}~p^2$ での $D$ の逆元*1 $E$ をとり $k\equiv(p-A)E~\mathrm{mod}~p^2$ （ $1\leq k\lt p^2$ ）と置くと

$A+kD=A+(p-A)ED\equiv p~\mathrm{mod}~p^2$

なので

$v_p(a+kd)=v_p(p^n(A+kD))=n+1$

となり、 $a$ と $a+kd$ が同色であることに矛盾する。

以上から $v_p(a)\lt v_p(d)$ なので $v_p(a+d)=v_p(a)$ 。これが任意の $p$ について成り立つので $a=a+d$ となり矛盾する。ゆえに素数は無限個存在する。 $~~~\square$

綺麗な証明かと言われれば微妙ですが、これはこれで面白い気がしませんか？

*1: $DE\equiv 1~\mathrm{mod}~p^2$ なる数

2017-08-04

格子点を2色で塗り分ける問題

組み合わせ論

先日、Twitterで次のような問題を見かけました。

問題. 平面上の格子点（座標が整数の点）を2色で塗り分ける。どのように塗っても、辺が $x,y$ 軸に平行で4つの頂点が同色の正方形が存在することを示せ。

その日の夜ベッドで考えながら寝たところ、朝起きて5分ほどで思いがけず綺麗に解くことができたので、解法を紹介したいと思います。証明のアイディアは下の記事に取り上げられているVan der Waerdenの定理に似ています。

integers.hatenablog.com

同色の正方形を作る前に、同色の「L字型」（正方形の右上以外の頂点）を作りましょう。実はこれは何色で塗り分けても存在します。

f:id:fibonacci_freak:20170802121415p:plain

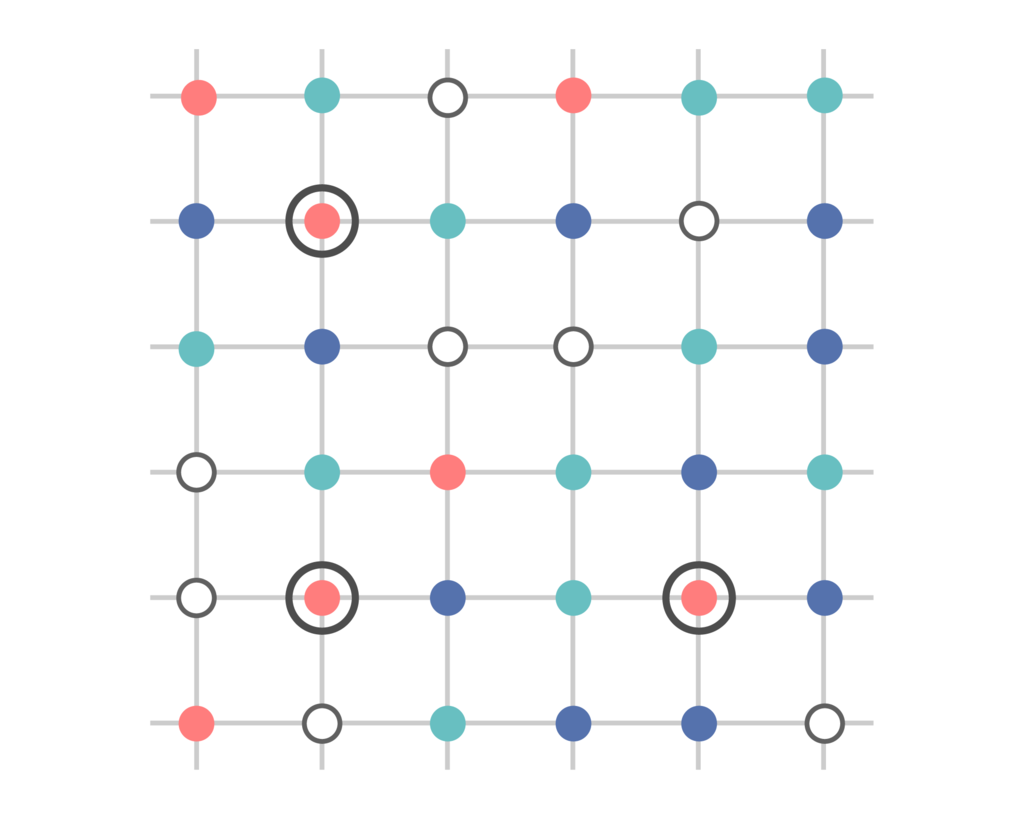
同色のL字型が無いと仮定します。すると実は十分大きい正方形領域をとれば、下図のような「左上の頂点を共有する $k-1$ 個のL字型の集まりで、各段の色が異なるもの」を見つけることができるのです。このような点の集まりををわかりやすく「 $k$ 段のオブジェ」と呼び、左上の頂点をその先端と呼ぶことにしましょう。

f:id:fibonacci_freak:20170802122808p:plain

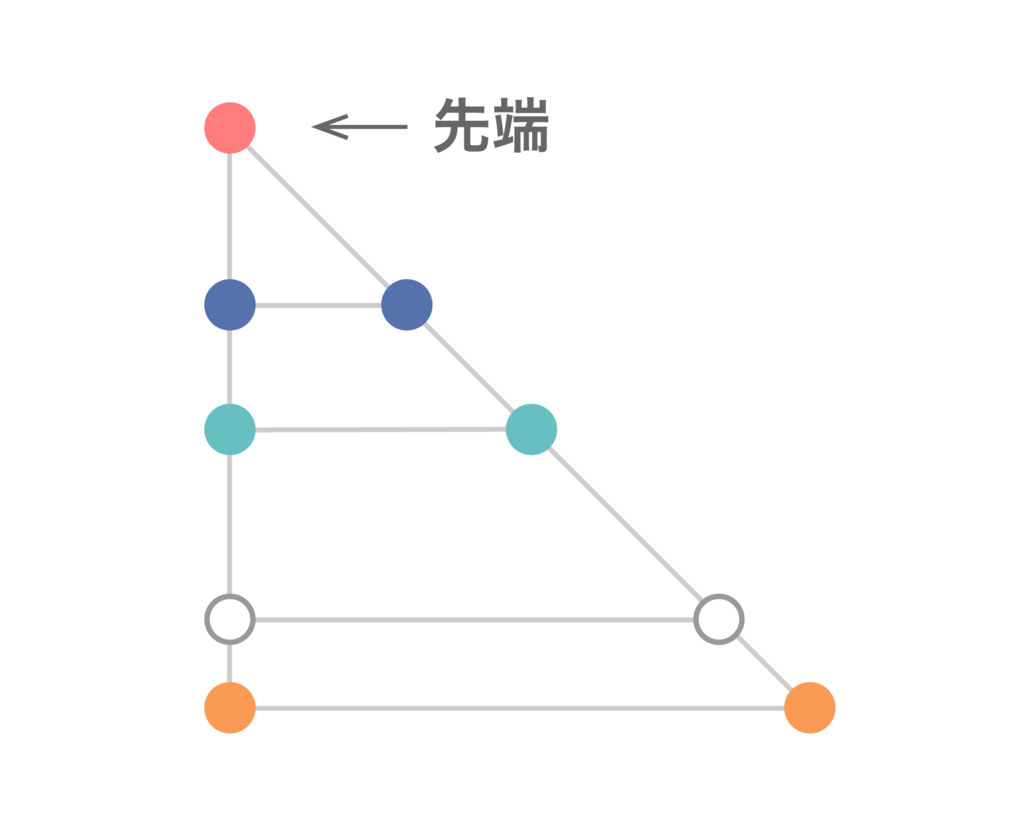
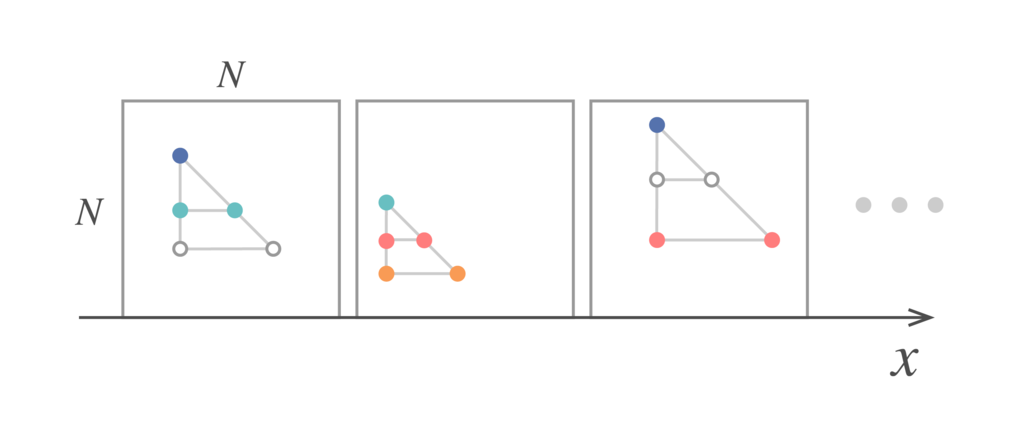
さて、実際に $k$ 段のオブジェを見つける方法を帰納的に示します。 $k=1$ のときは任意に1点とればそれが $1$ 段のオブジェになります。 $k\gt 1$ のとき、帰納法の仮定によりある整数 $N$ について $N\times N$ の正方形領域をとれば必ずその中に $k-1$ 段のオブジェが存在します。そこで $N\times N$ の正方形の列を $x$ 軸に平行にとり、それぞれの正方形に含まれる $k-1$ 段のオブジェを1つずつ選びます。そしてこれらの正方形に「選んだオブジェの配色と配置」を記したラベルをつけます。するとラベルの種類は有限なので、同じラベルのついた2つの正方形を取ることができます。

f:id:fibonacci_freak:20170802124137p:plain

これで同じ配色の $k-1$ 段のオブジェが横に2つ並んだ状況ができました。このときオブジェの先端2つとL字型をなす点 $P$ をとると、 $P$ はオブジェの各段の点ともL字型をなしているので、「同色のL字型が無い」という仮定よりオブジェに含まれるどの色とも異なる色で塗られていなければなりません。よって $P$ と2つのオブジェを合わせれば $k$ 段のオブジェができます。

f:id:fibonacci_freak:20170802124934p:plain

このように任意の段数のオブジェを作ることができるのですが、使う色は有限種類なのでそれより多い段数のオブジェを作ることはできず、矛盾します。これで同色のL字型が存在することが示せました！

2色の場合に戻りましょう。L字型が取れれば、正方形を見つけるのは簡単です。上に書いたことよりある整数 $M$ について、 $M\times M$ の正方形領域には必ず同色のL字型があります。そこで平面を $M\times M$ の正方形たちに分割し、各々に含まれる同色のL字型を1つずつ選んで、その色と配置を記したラベルをつけます。正方形たちを格子点とみなしラベルを色とみなすと、再び上に書いたことより、L字型に並んだ同じラベルの正方形3つを見つけることができます。このとき各正方形内のL字型を集めれば、下図左のように全て同色のL字型がL字型に並んだものが得られます。わかりやすいように、これらL字型の色を青, もう片方の色を赤とします。

f:id:fibonacci_freak:20170802130606p:plain

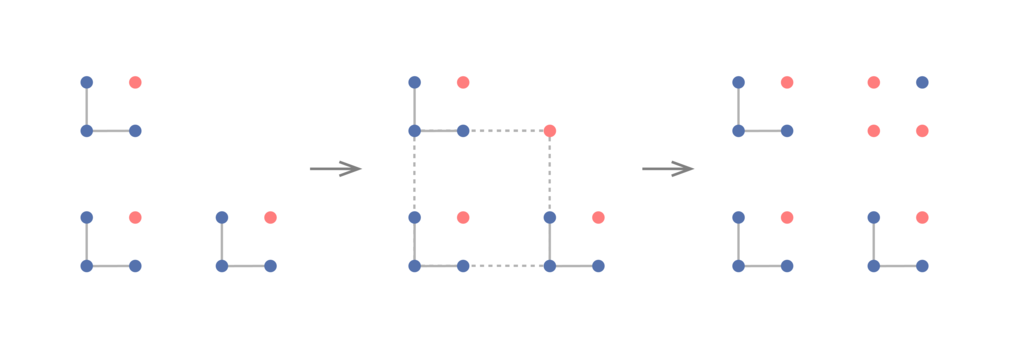
同色の正方形が存在しないとすると、小さいL字型の右上は赤となります（左）。また破線の正方形の右上の頂点も赤でなくてはいけません（中）。同じように右上の4点の色が定まります（右）。このとき一番外側の正方形は全て青で塗られており矛盾します。よって同色の正方形が存在することが示されました。

2017-08-01

グラフと素数：Erdős-Evansの定理

組み合わせ論素数

$0$ から $n-1$ までの整数から相異なる数 $a_1,\cdots,a_r$ を取り、「 $a_i-a_j$ が $n$ と互いに素なら $a_i,a_j$ を結ぶ」という規則で $a_i$ たちを頂点とするグラフを作ってみましょう。例えば $n=8$ として $0,1,2,5,7$ を選ぶと下のようなグラフが得られます（小さい数字は $|a_i-a_j|$ ）。

f:id:fibonacci_freak:20170728000103p:plain

グラフ $G$ をこのような方法で作ることができるとき、 $G$ は $\mathrm{mod}~n$ で表現可能であると言います。

ではどんなグラフが $\mathrm{mod}~n$ で表現可能なのでしょうか。

例えば $n$ を大きな素数として $0,1,\cdots,r-1$ を選べば完全グラフ $K_r$ を作ることができます。また $n=r!$ として $0,1,\cdots,r-1$ を選べば鎖状のグラフが得られます。

サイクルを作るのは少し難しいです。Twitterでこれを出題したところ、＠rudjereverisさんからとてもエレガントな解法を寄せて頂いたのでここで紹介します（私の想定解は間違っていることに後で気づきました…）。

大きな整数 $M$ をとって $n=3\times5\times7\times\cdots\times(2M+1)$ とします。すると考えている範囲で「 $n$ と互いに素 $\Leftrightarrow2$ 冪」としてよいことになります。このとき $0,1,3,7,\cdots,2^i-1, \cdots,2^r-1,2^r$ をとると、これは長さ $r+2$ のサイクルになっています。

さて、本題に入りましょう。実は次の驚くべき事実が成り立ちます！

定理(Erdős-Evans,1989). 任意のグラフはある $n$ に対し $\mathrm{mod}~n$ で表現可能である。

証明のために補題を準備します。

補題. 任意の正整数 $n$ について、 $n$ 個の素数からなる集合 $S$ で次の条件を満たすものが存在する:
【条件】共通部分を持たない任意の部分集合 $A,B\subset S$ について

$\displaystyle{\prod_{p\in A}p-\prod_{q\in B}q}$

は $\prod_{p\in S}p$ と互いに素。

証明. $n$ を固定し、条件を満たす $k$ 個の素数からなる集合で、全ての要素が $3^n$ 以上のもの $S_k$ を帰納的に構成していく。 $k=1$ の時は $3^n$ 以上の素数を任意に取れば良い。 $k\gt1$ の時、新たに加える素数 $p_k$ が満たすべき条件は

$\displaystyle{p_i\nmid p_k\prod_{p\in A}p-\prod_{q\in B}q}$

が任意の $1\leq i\lt k, A,B\subset S_{k-1}(A\cap B=\emptyset)$ に対し成り立つことである。 $p_i\in A$ なら必ず成り立つからそうでない場合のみ考えると、これは

$\displaystyle {p_k\not\equiv\frac{\prod_{q\in B}q}{\prod_{p\in A}p}~\mathrm{mod}~p_i}$

と同値である。右辺の組み合わせは高々 $3^{k-1}(\lt 3^n\leq p_i)$ 通りしかないので、これらをすべて満たす $\mathrm{mod}~p_i$ の剰余類が存在する。中国剰余定理によって $i$ をすべて合わせて考えれば、 $p_k$ はある等差数列中にあればよいことになる。よって算術級数定理より条件をみたす十分大きい $p_k$ を取ることができる。 $~~~\square$

それでは定理を示しましょう。

定理の証明. 表現したいグラフ $G$ に1つの頂点を加え、その補グラフ（辺で結ばれているかどうかを全て反転したグラフ）を $H$ とする。 $H$ の辺の数を $m$ とし、補題の条件を満たす $m$ 個の素数からなる集合 $S$ をとり、各辺に1つずつ素数を割り当てる。 $n=\prod_{p\in S}p$ とし、 $G$ の各頂点に対し「 $H$ で自分に繋がっている辺に割り当てられた素数の積」を選べばよい。 $~~~\square$

如何でしたでしょうか。この証明は美しいですが、算術級数定理を使っているところが少し残念かもしれません。もっと初等的に示せた方がいましたら、ぜひ教えてください。

2017-07-29

2^n+1を割り切る素数の密度は17/24

素数

$2^n+1(n\geq1)$ という数列を考えましょう。

$3,5,9,17,33,65,129,257,\cdots$

これは全て奇数ですから $2$ の倍数は登場しません。 $3,5,11,13,17$ の倍数は上の列に出てきていますね。しかし $7$ の倍数は見当たりません。実はこの列には $7$ の倍数は現れないのです。これは $2^n~\mathrm{mod}~7$ が

$2,4,1,2,4,1,\cdots$

と循環し、 $6$ が現れないことからわかります。

では、 $2^n+1$ の素因数に現れる素数は、素数全体のうちどのくらいあるのでしょうか？

実はHasseによる次の定理(1966)があります。

定理. ある $n\geq1$ について $2^n+1$ を割り切る素数の密度は $\dfrac{17}{24}$ である。

ここで密度とは、 $x$ 以下の素数の個数をを $\pi(x)$ 、その中で条件を満たす素数の個数を $\pi'(x)$ とするとき

$\displaystyle{\lim_{x\to \infty}\frac{\pi'(x)}{\pi(x)}}$

のこと（いわゆる自然密度）とします。

17という数が出てくるところが面白いですね。

今回はこの定理の証明をしたいと思いますが、初等的な証明ではないので、代数的整数論の基本的な知識（円分体における素イデアルの分解など）を仮定します。これについては以下のtsujimotterさんのブログにわかりやすい解説があるので、あまり詳しくない方はそちらも参照してみてください。

tsujimotter.hatenablog.com

さて、ある条件を満たす素数の密度を計算する方法はどんなものがあるでしょうか？

整数論に詳しい人なら、その一つとして真っ先にChebotarevの密度定理を挙げるでしょう。あるいはその特別な場合である次の定理が有名です。

命題1. Galois拡大 $K/\mathbb{Q}$ で完全分解する素数の密度は $\dfrac{1}{[K:\mathbb{Q}]}$ である。

証明は省略しますが、比較的簡単なので今後このブログで紹介するかもしれません。

Hasseによる証明では、素数が $2^n+1$ を割り切るという条件をある代数体における完全分解という条件に書き直すことで、命題1に帰着させるのです。まずはこの書き換えをしていきましょう。議論を簡単にするため、素数は奇素数のみ考えます（こうしても密度には影響しません）。

素数 $p$ が条件を満たさない、つまり $2^n\equiv-1~\mathrm{mod}~p$ が解を持たないためには、 $\mathbb{F}_p^\times\cong \mathbb{Z}/(p-1)\mathbb{Z}$ における $2$ の位数が奇数であることが必要十分です。ここで次の補題を使います。

補題. $\mathrm{ord}_2(p-1)=j$ とする。 $\mathbb{F}_p^\times$ における $a$ の位数が奇数である必要十分条件は

$x^{2^j}\equiv a~\mathrm{mod}~p\tag{1}$

が解を持つことである。

証明. (1)が解を持つならば $a^{(p-1)/2^j}\equiv x^{p-1}\equiv 1~\mathrm{mod}~p$ だから、 $a$ の位数は $(p-1)/2^j$ を割り切り、奇数である。逆に $a$ の位数が奇数 $2m+1$ ならば、原始根 $r$ をとって $a=r^k$ とすると $a^{2m+1}\equiv r^{k(2m+1)}\equiv1~\mathrm{mod}~p$ なので $2^j\mid k$ となり解 $r^{k/2^j}$ が得られる。 $~~~\square$

$2^j\mid p-1$ より $\mathbb{F}_p$ には $1$ の $2^j$ 乗根が全てあるので、上の方程式が解を持つことは

$x^{2^j}-2=(x-a_1)\cdots(x-a_{2^j})~\mathrm{mod}~p$

と一次式の積に分解することと同値です。以上で次が得られました。

命題2. $^\forall n,~p\nmid 2^n+1$ かつ $\mathrm{ord}_2(p-1)=j ~\Leftrightarrow~ p$ が $\mathbb{Q}(\sqrt[2^j]{2})$ で完全分解かつ $\mathrm{ord}_2(p-1)=j.$

次に $\mathrm{ord}_2(p-1)=j$ の部分を書き換えましょう。これは

$p\equiv 1~\mathrm{mod}~2^j$ かつ $p\not\equiv 1~\mathrm{mod}~2^{j+1}$

と同値です。円分体における素イデアルの分解法則より、上の条件は

$p$ は $\mathbb{Q}(\zeta_{2^j})$ で完全分解するが $\mathbb{Q}(\zeta_{2^{j+1}})$ では完全分解しない

と言い換えられます（ $\zeta_n$ は $1$ の原始 $n$ 乗根）。ここで2つの $\mathbb{Q}$ 上Galois拡大体の系列 $K_j.L_j(j\geq 1)$ を

$K_j=\mathbb{Q}(\zeta_{2^j},\sqrt[2^j]{2})\\L_j=\mathbb{Q}(\zeta_{2^{j+1}},\sqrt[2^j]{2})$

と定めます。一般に「合成体 $LK$ で完全分解 $\Leftrightarrow L,K$ で完全分解」であることに注意すれば、結局次が得られたことになります。

命題3. $^\forall n,~p\nmid 2^n+1$ かつ $\mathrm{ord}_2(p-1)=j ~\Leftrightarrow~ p$ は $K_j$ で完全分解するが $L_j$ で完全分解しない。

命題1と組み合わせることで次が得られます。

命題4. ある $n\geq1$ について $2^n+1$ を割り切る素数の密度は

$\displaystyle{1-\sum_{j=1}^\infty\left(\frac{1}{[K_j:\mathbb{Q}]}-\frac{1}{[L_j:\mathbb{Q}]}\right).}$

これで問題は拡大次数 $[K_j:\mathbb{Q}],[L_j:\mathbb{Q}]$ を求めることに帰着されました！

$K_j$ から求めていきましょう。 $j=1$ のとき $2$ 次、 $j=2$ のとき $8$ 次拡大であることは簡単にわかります。 $j\geq3$ の場合、 $[\mathbb{Q}(\zeta_{2^j}):\mathbb{Q}]=\phi(2^j)=2^{j-1}$ なので、 $[\mathbb{Q}(\sqrt[2^j]{2}):\mathbb{Q}(\zeta_{2^j})]$ を求めます。

$C_j=\mathbb{Q}(\zeta_{2^j}),\alpha:=\sqrt2$ と置きます。 $\alpha=\zeta_8+\zeta_8^{-1}\in C_j$ なので上の拡大はKummer拡大 $C_j(\sqrt[2^{j-1}]{\alpha})/C_j$ であり、Kummer理論より拡大次数は $\langle\alpha\rangle\subset C^\times/(C^\times)^{2^{j-1}}$ の位数に等しくなります。ここで $\sqrt[4]{2}\not\in C_j$ *1より $k\lt j-1$ のとき $\alpha^{2^k}\not\in (C^\times)^{2^{j-1}}$ なので、拡大次数は $2^{j-1}$ とわかりました。よって

$[K_j:\mathbb{Q}]=2^{j-1}\cdot2^{j-1}=2^{2j-2}.$

同様に $L_j$ についても $j=1$ のとき $4$ 次拡大であり、 $j\geq2$ の時はKummer拡大 $C_{j+1}(\sqrt[2^{j-1}]{2})/C_{j+1}$ の次数が $2^{j-1}$ なので

$[L_j:\mathbb{Q}]=2^j\cdot2^{j-1}=2^{2j-1}.$

以上をまとめると次のようになります。

$j$	$1$	$2$	$\geq3$
$[K_j:\mathbb{Q}]$	$2$	$8$	$2^{2j-2}$
$[L_j:\mathbb{Q}]$	$4$	$8$	$2^{2j-1}$

それでは密度を求めてみましょう。

$\displaystyle{1-\sum_{j=1}^\infty\left(\frac{1}{[K_j:\mathbb{Q}]}-\frac{1}{[L_j:\mathbb{Q}]}\right)\\=1-\left(\frac{1}{2}-\frac{1}{4}\right)-\left(\frac{1}{8}-\frac{1}{8}\right)-\sum_{j=3}^\infty \left(\frac{1}{2^{2j-2}}-\frac{1}{2^{2j-1}}\right)\\=\frac{3}{4}-\sum_{j=3}^\infty \frac{2}{4^j}\\=\frac{3}{4}-\frac{2\cdot\frac{1}{64}}{1-\frac{1}{4}}\\=\frac{17}{24}.}$

ちゃんと $\dfrac{17}{24}$ が出てきましたね！これでHasseの定理の証明が完了しました。

実は私が最近読んだ論文の中に「Lucas数を割り切る素数の密度は $\dfrac{2}{3}$ である」という定理があって、その中に上の結果と証明が紹介されていたというのが今回の記事の経緯です。Lucas数の方の結果も同じように素イデアル分解の条件に書き直して密度定理を使うことで証明できるようです。

*1: $C_j(\sqrt[4]{2})$ が $\mathbb{Q}$ の非Abel拡大 $K_2=\mathbb{Q}(i,\sqrt[4]{2})$ を含むことからわかります。

2017-07-28

とある整数論の問題と、その鮮やかな解法

次の問題は1984年にハンガリーのとある数学コンテストで出題されたものです。

問題. $a,b$ を正整数とする。どんな素数 $p$ についても $a$ を $p$ で割った余りが $b$ を $p$ で割った余り以下であるとき、 $a=b$ を示せ。

これはもともとPálfyという数学者が予想し、ErdősがSylvester-Shurの定理から従うことを指摘したという経緯があります。しかしこれを数学コンテストに出題したところ、Szegedyという学生が簡潔でself-containdな解法を発見しました。その後、彼ら3人はその解法を共著論文にまとめています。今回はそのエレガントな解法を紹介したいと思います。

以下 $a,b$ を $p$ で割った余りを $a_p,b_p$ と書きます。

問題の解答. $a\neq b$ と仮定する。まず $p$ を十分大きくとることで $a\lt b$ がわかる。さらに $a$ を $b-a$ に変えても仮定は保たれるから、最初から $1\leq a\leq b/2$ としてよい。

$A=1\cdot2\cdots (a-1)a\\B=(b-a+1)\cdots (b-1)b$

と置く。また $\alpha(p^k),\beta(p^k)$ を $A,B$ それぞれの因子（掛けられている $a$ 個の数）のうち $p^k$ で割れるものの個数とする。すると

$\displaystyle{A=\prod_p p^{\sum_{k=1}^\infty\alpha(p^k)},~B=\prod_p p^{\sum_{k=1}^\infty\beta(p^k)}.}$

ここで $A,B$ の因子はどちらも $a$ 個の連続した自然数だから $|\alpha(p^k)-\beta(p^k)|\leq1$ がわかる。さらに $A,B$ の因子を大きい方から順に見ていくと、問題の仮定 $a_p\leq b_p$ より $A$ の因子の方が先に $p$ で割れるから $\alpha(p)\geq \beta(p)$ である。とくに $p\gt a$ ならば $\alpha(p)=\beta(p)=0$ である。ゆえに上の式は

$\displaystyle{\frac{B}{A}=\prod_{p\leq a} p^{\sum_{k=1}^\infty(\beta(p^k)-\alpha(p^k))}}$

となる。 $\beta(p^k)\gt 0$ となる最大の $k$ を $\kappa(p)$ と置くと上の指数部分は

$\displaystyle{\sum_{k=1}^\infty(\beta(p^k)-\alpha(p^k))=(\beta(p)-\alpha(p))+\sum_{k=2}^{\kappa(p)}(\beta(p^k)-\alpha(p^k))-\sum_{k=\kappa(p)+1}^\infty \alpha(p^k)\\ \leq 0+\sum_{k=2}^{\kappa(p)}1=\kappa(p)-1}$

と評価できるから

$\displaystyle{\frac{B}{A}\biggm\vert \prod_{p\leq a}p^{\kappa(p)-1}}.$

変形すると

$\displaystyle{\frac{(b-a+1)\cdots (b-1)b}{\prod_{p\leq a}p^{\kappa(p)}}\biggm\vert\frac{1\cdot2\cdots(a-1)a}{\prod_{p\leq a}p}}$

となる（両辺は整数になっている）。左辺分子の因子のうち約分されるものは高々 $\pi(a)$ 個（ $\pi(n)$ は $n$ 以下の素数の個数）なので

$(左辺)\geq(b-a+1)^{a-\pi(a)}.$

一方右辺分子の因子はちょうど $\pi(a)$ 個約分されるので

$(右辺)\leq a^{a-\pi(a)}.$

よって $b-a+1\leq a$ .これは最初に課した仮定 $b\geq2a$ に矛盾している。よって $a=b$ が示された。 $~~~\square$

まさに見事な証明と言うほかありません。この証明を部屋に飾って眺めていたいくらいです。いつかこんな証明がしてみたいですね。

2017-07-26

Fibonacci素数とF-完全数

Fibonacci 素数

完全数とは「自分自身以外の約数の総和が自分自身になる」ような正整数のことで、 $6,28,496,8128,\cdots$ と続きます。

これの仲間として「自分自身以外の約数の2乗和が自分自身の3倍になる」ような正整数を「F-完全数」と呼ぶことにしましょう。最初の3つのF-完全数は

$10\to 1^2+2^2+5^2=30=10\times 3\\65\to 1^2+5^2+13^2=195=65\times 3\\20737\to 1^2+89^2+233^2=62211=20737\times 3$

となります。

ところでこれらの数の約数を眺めていると不思議なことに気がつきます。そう、 $2,5,13,89,233$ は全てFibonacci数になっているのです。

種明かしをすると、実は次の定理が成り立つのです（Cai-Chen-Zhang,2015）。

定理. $n$ がF-完全数である必要十分条件は、共に素数である2つのFibonacci数 $F_{2m-1}, F_{2m+1}$ を用いて $n=F_{2m-1}F_{2m+1}$ と表されることである。

これを証明するためにLucas数について簡単な性質を確認しておきましょう。Lucas数とはFibonacci数の仲間で、 $L_1=1,L_2=3,L_{n+2}=L_{n+1}+L_n$ で定義されます。一般項を求めると次のようにまとめられます（証明略）。

補題. $\dfrac{L_n+F_n\sqrt5}{2}=\left(\dfrac{1+\sqrt5}{2}\right)^n.$

またFibonacci数との間には以下の関係があります。

補題. $L_n=F_{n+1}+F_{n-1}.$

これは帰納法により簡単に示すことができます。

それでは定理を示しましょう！

定理の証明. $n$ の約数が5個以上あったとし、小さい方から2つめ,3つめのものを $d_1, d_2$ とすると、相加相乗平均の不等式より

$1^2+d_1^2+(n/d_1)^2+d_2^2+(n/d_2)^2\geq1+2n+2n=1+4n$

となり不適。逆に約数が3個以下でも明らかに不適。ゆえに約数はちょうど4個なので、 $n=pq$ または $n=p^3$ （ $p,q$ は素数）と書ける。後者の場合約数の2乗和は $1+p^2+p^4\gt p\cdot p^3$ となるから $p\geq3$ では不適で、 $p=2$ でも成り立たない。よって $n=pq$ となる。