2017-08-26

HEXは先手必勝である

組み合わせ論

HEXは以下の記事で紹介したボードゲームです。

fibonacci-freak.hatenablog.com

実はHEXは先手必勝であることが知られています。このこともまた、ゲームの考案者の1人であるNashが証明しました。

しかもその証明法はあまりにも意外です。ふつう先手必勝といえば「各ターンでこういう手を打てば勝てる」という必勝法を見つけようと考えるでしょう。しかしなんとHEXにおいては具体的な必勝法はわからないのです。

今回はその不思議で圧倒的な証明を紹介したいと思います。

注意: ドロップダウンの中に証明があります。自分で考えてみたい方は見てしまわないようにご注意ください。

定理. HEXは先手必勝である。

証明. 背理法で示す。先手必勝でないならば後手必勝である（HEXの定理と、残り手数についての帰納法でわかる）。この仮定のもとで先手の戦略を考える。先手は初手はどこを塗ってもよい。この一手を無視し、先手は後手の必勝手順の通りにゲームを進める。ただし途中で塗るべきタイルが既に塗られている場合はどこを塗ってもよい。このとき先手は必勝手順よりさらに1手分得をしているので必ず勝つことができる。これは後手必勝に矛盾している。ゆえに先手必勝である。 $~~~\square$

このような議論はstrategy stealing argumentと言われていて、他にも様々なゲームに応用できます。しかしこんな証明は人間には思いつかないように思われます。Nashは宇宙人だったのでしょう。

2017-08-25

HEXの定理(2)

組み合わせ論

この記事は以下の記事の続きです:

fibonacci-freak.hatenablog.com

さて、前回はHEXの定理とBrouwerの不動点定理が実は同値であるということを紹介しました。今回はその証明を書こうと思います。それぞれのステートメントを確認しておきましょう。

定理(HEXの定理). HEXに引き分けは存在しない。すなわち全てのタイルが塗られていれば、どちらかの色は自陣をつないでいる。

定理(Brouwerの不動点定理). $D=[0,1]^2$ とすると、任意の連続写像 $f:D\to D$ は不動点（ $f(x)=x$ なる点）をもつ。

証明のための第一歩はHEXの定理の次のような言い換えです。

命題. 下図のようなグラフ $G_n$ の頂点を赤と青の2色で塗り分ける。このとき次のいずれかが存在する。
(1)上下の辺を結ぶ道で赤い頂点からなるもの。
(2)左右の辺を結ぶ道で青い頂点からなるもの。

f:id:fibonacci_freak:20170824231208p:plain

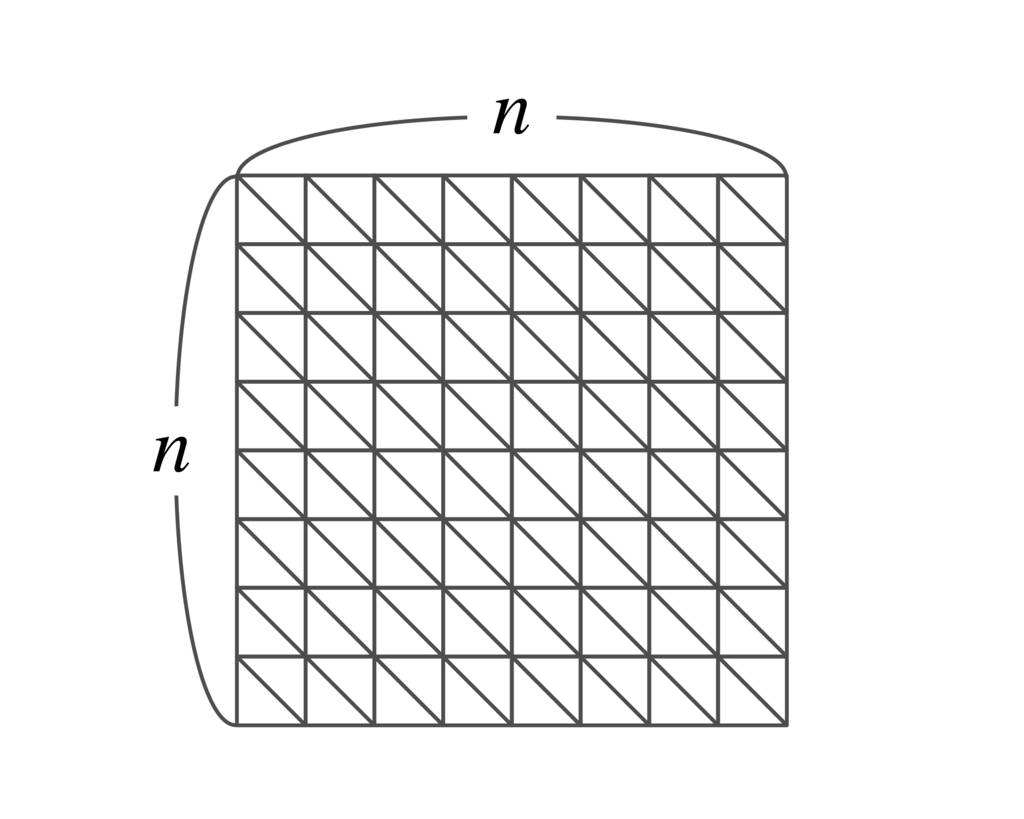
HEXの盤面をそのままグラフに直せば、これがHEXの定理と同値であることがわかります。

それでは不動点定理との同値性を証明しましょう。

HEXの定理 $\Rightarrow$ 不動点定理.

$f:D\to D$ に不動点が存在しないと仮定する。 $|f(x)-x|$ は $D$ 上で最小値を持つのでそれを $\varepsilon\gt0$ とする。また上図のグラフ $G_n$ を、上下左右の辺が $D$ の上下左右の辺上に来るように $D$ 内に配置する。このときグラフ上の任意の点について $f$ による $x$ 座標, $y$ 座標の変化のいずれかは $\varepsilon/2$ 以上なので、前者なら赤に、後者なら青に塗る。両方を満たす場合はどちらに塗ってもよい。上の命題より上下の辺を結ぶ赤い頂点からなる道があるとしても一般性を失わない。

さらにこの道上の頂点を、 $f$ により $y$ 座標が $\varepsilon/2$ 以上減少するならば白、増加するならば黒で塗り分ける。道の上端の点は白、下端の点は黒なので、道中の連続する2点 $A,B$ で色が異なるものが存在する。 $n$ を十分大きくとれば $|A-B|$ は任意に小さくでき、かつ $|f(A)-f(B)|\gt\varepsilon/2$ とできる。これは $f$ の一様連続性に反する。 $~~~\square$

不動点定理 $\Rightarrow$ HEXの定理.

上と同様に $D$ に $G_n$ を埋め込む。命題の(1)(2)いずれも成立しない塗り分けがあったとすると、頂点集合には以下の4つの交わらない部分集合が存在する。

$N=\{$ 上の辺からの赤い道がある赤い頂点 $\}$

$S=\{N$ に属さない赤い頂点 $\}$

$W=\{$ 左の辺からの青い道がある青い頂点 $\}$

$E=\{W$ に属さない青い頂点 $\}$

そして十分小さい $\varepsilon\gt 0$ をとり、 $g:V(G_n)\to D$ （ $V(G)$ は $G$ の頂点集合を表す）を以下のように定める。

$v_1=\dbinom{0}{\varepsilon}, v_2=\dbinom{\varepsilon}{0}$

$g(P)=\begin{cases}P-v_2~~(P\in N)\\P+v_2~~(P\in S)\\P+v_1~~(P\in W)\\P-v_1~~(P\in E)\end{cases}$

ただし仮定から $g$ の像は $D$ に入ることに注意する。

$g$ を小三角形ごとに線形に補間することで連続写像 $f:D\to D$ が得られる。不動点定理より $f$ の不動点 $x$ が存在する。 $x$ を内部に含む $G_n$ の小三角形の頂点 $P_1,P_2,P_3$ を取ると、 $\{f(P_i)-P_i\}$ の凸包は原点を含むので、これらの頂点は $N,S,W,E$ のうち相異なる3つに属する。 $P_1,P_2$ がそれぞれ $N,S$ に属するとしても一般性を失わない。しかし $P_1,P_2$ は辺で結ばれているから $P_2$ は上の辺からの赤い道があることになり $P_2\in S$ に矛盾する。 $~~~\square$

組み合わせ論と位相幾何の間のアナロジーは多々ありますが、このように綺麗に同値になる例は少ないように思います。

2017-08-19

HEXの定理(1)

組み合わせ論

HEXというボードゲームを知っていますか？

1940年代に作られたゲームなのですが、最近はスマホのアプリにもなっているようです。私が高校生の頃はよく同級生が遊んでいました。

HEXは六角形のタイルが敷き詰められたひし形の盤で遊びます。2人で交互にタイルを自分の色（赤か青）で塗り、自陣である向かい合う辺を自分の色のタイルでつないだ方が勝ちとなります。言葉で説明するのは難しいので、下の図を見てください。

f:id:fibonacci_freak:20170819110646p:plain

図の場合、赤が上下の赤の陣地をつないでいるので赤の勝ちとなります。

ここで自然に湧く疑問があります。

赤も青も勝たないまま全てのタイルが塗られてしまうことはあるのか？

つまり、HEXに引き分けはあるのか？

結論から言うと、HEXに引き分けはありません。このことはHEXの考案者の1人であるNash（ゲーム理論で有名なあのNashです！）自身が証明し、HEXの定理と呼ばれています。

定理. HEXに引き分けは存在しない。すなわち全てのタイルが塗られていれば、どちらかの色は自陣をつないでいる。

証明. 便宜上、盤の外も自陣の色を延長して赤と青で塗られているとする。赤と青の接する境界線を全て描く（下図の白線）。

f:id:fibonacci_freak:20170819111526p:plain

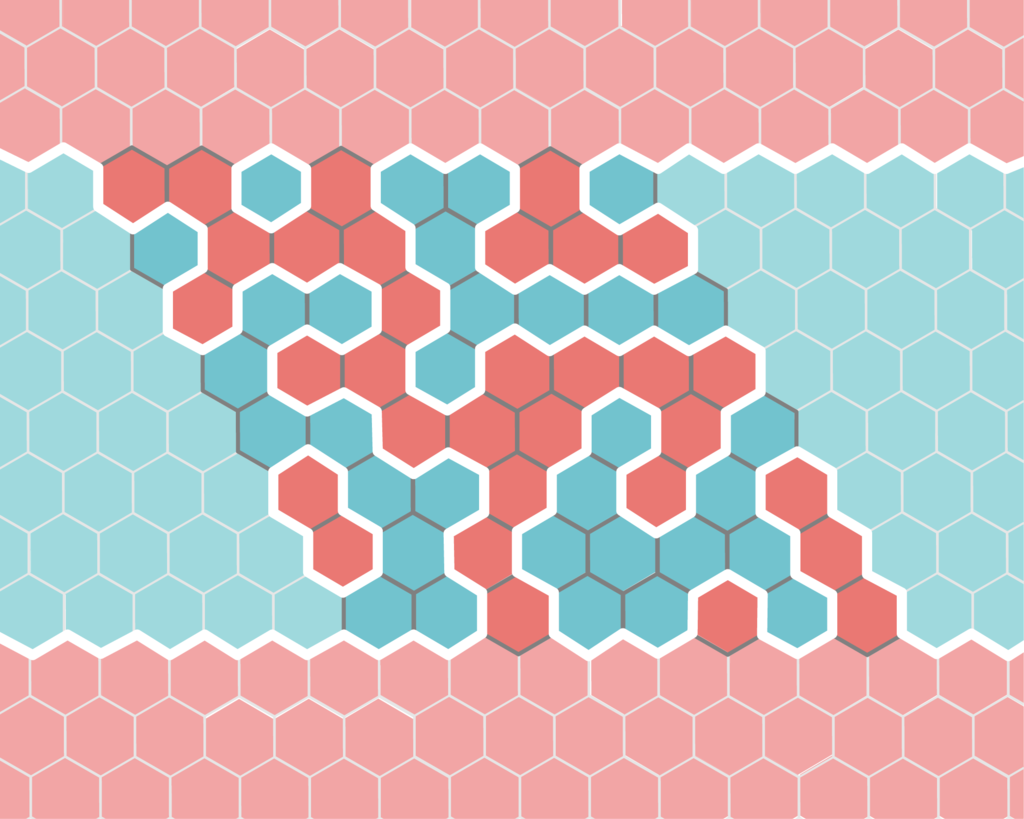
曲がり角の塗られ方を考えれば、この線は途中で切れたり分岐したりしないことがわかる。よって図の左右から出ている4本の境界線は2本ずつ結ばれることになる。すなわち下図のいずれかのようになる。

f:id:fibonacci_freak:20170819113203p:plain

f:id:fibonacci_freak:20170819113232p:plain

左の場合は青、右の場合は赤が勝っている。 $~~~\square$

スマートな証明ですね。

しかしHEXの定理の面白さはその証明だけにとどまりません。なんとHEXの定理は2次元におけるBrouwerの不動点定理と同値なのです！

定理(Brouwerの不動点定理). $D=[0,1]^2$ とすると、任意の連続写像 $f:D\to D$ は不動点（ $f(x)=x$ なる点）をもつ。

ここで証明を紹介したいのですが、とても面白い証明なので、まずは是非皆さん自身で考えてみてください（私自身は考える前に証明を読んでしまい少し悔しい思いをしました）。意外と素直に証明できます。ヒントが欲しい方はTwitterなどで連絡してください。

証明は次の「HEXの定理(2)」で紹介します。お楽しみに！

2017-08-17

痩せた集合・太った集合

私は痩せています。どのくらい痩せているかというと、アスパラぐらいです。

実は数学には「痩せた集合」という概念があって、私はだいぶ親近感を持っています。今日はその痩せた集合について書きたいと思います。

まずは痩せた集合の定義をしましょう。

定義. $X$ を位相空間、 $A$ をその部分集合とする。
(1) $A$ が稀薄であるとは、 $A$ の閉包が内点を持たないことをいう。
(2) $A$ が痩せた集合（または第1類集合）であるとは、高々可算個の稀薄な集合の合併として表せることをいう。
(3) $A$ が太った集合（または第2類集合）であるとは、痩せた集合でないことをいう。

今回は位相空間と言ったら実数 $\mathbb{R}$ や区間 $[0,1]$ などのことだと思っても差し支えありません。また太った集合というのはここだけのネーミングで、一般的ではありません。

例えば $X=[0,1]$ とすると、 $A=\{\frac{1}{n}\mid n\in\mathbb{Z}_{\gt 0}\}\cup \{0\}$ は内点を持たない閉集合なので稀薄な集合で、とくに痩せた集合です。また $[0,1]$ 自身は太った集合になります。このことは次のBaireの範疇定理からわかります。

定理(Baireの範疇定理). 完備距離空間の痩せた部分集合は内点を持たない。特に完備距離空間は（それ自身の部分集合として）太った集合である。

証明はいろんなところに書いてあるので省略します。

もう一つ痩せた集合の代表としてカントール集合が挙げられます。これは $[0,1]$ から始めて「つながった区間を3等分して真ん中の開区間を取り除く」という操作を無限回繰り返して得られる集合です。開区間を取り除いているので出来上がる集合は閉集合になります。

f:id:fibonacci_freak:20170816234845p:plain

真ん中を取り除くごとに連結成分1つ分の長さは $\dfrac{1}{3}$ になるので、内点を持たない（区間を含まない）、つまり痩せた集合であることがわかります。また真ん中を取り除くごとに測度（長さの合計）は $\dfrac{2}{3}$ になるので、カントール集合は測度0です。

さて、今回伝えたいのは「痩せた集合も結構すごい」という事実です。具体的には $[0,1]$ の部分集合で、痩せた集合にもかかわらず正の測度を持つものが存在するのです！

それが「太ったカントール集合」です。「太った」と付いていますが、これは「カントール集合に比べたら太っている」という意味で、実態は痩せた集合です。

太ったカントール集合の構成は簡単です。まず区間 $[0,1]$ から始めて、中央から長さ $\dfrac{1}{4}$ の開区間を取り除きます。次に残った2つの区間それぞれの中央から長さ $\dfrac{1}{16}$ の開区間を取り除きます。次は $\dfrac{1}{64}$ 、その次は $\dfrac{1}{256},\cdots$ と、 $\dfrac{1}{4^n}$ の開区間を次々に取り除いてきます。これを無限回繰り返したとき残る集合が太ったカントール集合です。

f:id:fibonacci_freak:20170817115815p:plain

これも区間を取り除くごとに連結成分1つ分の長さが半分以下になるので、内点を持たず、痩せた集合であることがわかります。

太ったカントール集合の測度は

$1-\dfrac{1}{4}-\dfrac{2}{16}-\dfrac{4}{64}-\cdots-\dfrac{2^n}{4^{n+1}}-\cdots\\=1-\left(\dfrac{1}{4}+\dfrac{1}{8}+\dfrac{1}{16}+\cdots\right)\\=\dfrac{1}{2}$

となり、確かに正の測度 $\dfrac{1}{2}$ を持ちます！人は見かけで判断してはいけないのです。私も実は正の測度を持っているかもしれません。

さらに、太った集合にもかかわらず測度が0の雑魚集合も存在します。これは次のように作ります。

まず太ったカントール集合 $S$ を用意します。 $S$ にはたくさんの「開区間の穴」が空いていますが、その全てに「 $S$ を相似縮小したもの」を詰め込みます。

f:id:fibonacci_freak:20170817115854p:plain

こうして得られたものを $S_1$ とします。さらに $S_1$ の全ての穴に $S$ を詰め込んだものを $S_2$ とし、 $S_3,S_4,\cdots$ と順に気持ち悪い集合を作っていきます。そして最後に

$\displaystyle{T=\bigcup_{n=1}^\infty S_n}$

とします。 $S$ を詰め込むたびに空白の部分の測度は半分ずつになるので、 $T$ の測度は $1$ になります。また各 $S_n$ は稀薄な集合なので $T$ は痩せた集合です。すると $T$ の補集合は太った集合で*1、かつ測度0になります。

如何でしたでしょうか。皆さんも是非自分好みの気持ち悪い例を作って遊んでみてください。

*1:補集合も痩せているとすると $[0,1]$ も痩せていることになりBaireの範疇定理に矛盾します。

2017-08-14

自作数学パズル保管所を開設しました

実は私は最近数学パズルを自作するのにハマっており、時々Twitterなどで出題しています。しかしTwitterではすぐに過去の問題が流れていってしまい、後から見つけるのが大変です。そこで自作パズルを別のブログにまとめておくことにしました。

parabolic-puzzles.hatenadiary.jp

（なぜかhatenablog.comではなくhatenadiary.jpになってしまい悲しいです）

みなさんぜひチャレンジしてください！

2017-08-13

素数の無限性の一風変わった証明

素数組み合わせ論

素数が無限に存在することはもはや人類の常識と言えますが、その証明を沢山知っている人は少ないように感じます。

私は証明そのものを鑑賞するのが好きなタイプなので、以前からずっと素数の無限性のオリジナル証明を作れないかと考えていたのですが、この間ついに組み合わせ論的な証明を思いつきました。組み合わせ論の最も美しい（？）定理の一つ、Van der Waerdenの定理を使う証明です。

定理(Van der Waerden). 正整数全体をどのように有限色で塗り分けても、任意の長さの同色の等差数列が存在する。

この定理の証明は以下の記事などに紹介されています。

integers.hatenablog.com

しかし残念なことに、関連するキーワードで検索したところ、私の考えたものとほぼ同じ証明が既に別の人（L. Alpoge氏）によって発表されていました。しかも私の証明には穴があって、彼の論文ではそれが埋められていることにも気づきました。数学の世界は厳しいですね！

そういうわけで悔しいのですが、せっかくなので今回は彼の証明を紹介したいと思います。今回の記事では正整数 $n$ が素数 $p$ で割れる回数を $v_p(n)$ で表します。

定理. 素数は無限に存在する。

証明. 素数が有限個だったと仮定すると、正整数全体を「素因数に現れる素数の種類とそれぞれの指数の偶奇」を色として塗り分けることができる。どの素数の2乗よりも大きい正整数 $r$ をとると、Van der Waerdenの定理より $a,a+d,\cdots,a+dr$ という同色の等差数列が存在する。このとき $a$ の任意の素因数 $p$ について $p\mid a+d$ だから $p\mid d$ 。

(1) $v_p(a)\gt v_p(d)$ とすると $v_p(a+d)=v_p(d)\lt v_p(a)$ なので、 $a$ と $d$ で $p$ の指数の偶奇が等しいことから $v_p(a)\gt v_p(d)+1$ 。このとき $v_p(a+pd)=v_p(pd)=v_p(d)+1$ となって、 $a+pd$ と $a+d$ が同色であることに矛盾する。

(2) $v_p(a)=v_p(d)$ とすると $a=p^nA$ , $d=p^nD$ （ $A,D$ は $p$ と互いに素）と書ける。 $\mathrm{mod}~p^2$ での $D$ の逆元*1 $E$ をとり $k\equiv(p-A)E~\mathrm{mod}~p^2$ （ $1\leq k\lt p^2$ ）と置くと

$A+kD=A+(p-A)ED\equiv p~\mathrm{mod}~p^2$

なので

$v_p(a+kd)=v_p(p^n(A+kD))=n+1$

となり、 $a$ と $a+kd$ が同色であることに矛盾する。

以上から $v_p(a)\lt v_p(d)$ なので $v_p(a+d)=v_p(a)$ 。これが任意の $p$ について成り立つので $a=a+d$ となり矛盾する。ゆえに素数は無限個存在する。 $~~~\square$

綺麗な証明かと言われれば微妙ですが、これはこれで面白い気がしませんか？

*1: $DE\equiv 1~\mathrm{mod}~p^2$ なる数

2017-08-04

格子点を2色で塗り分ける問題

組み合わせ論

先日、Twitterで次のような問題を見かけました。

問題. 平面上の格子点（座標が整数の点）を2色で塗り分ける。どのように塗っても、辺が $x,y$ 軸に平行で4つの頂点が同色の正方形が存在することを示せ。

その日の夜ベッドで考えながら寝たところ、朝起きて5分ほどで思いがけず綺麗に解くことができたので、解法を紹介したいと思います。証明のアイディアは下の記事に取り上げられているVan der Waerdenの定理に似ています。

integers.hatenablog.com

同色の正方形を作る前に、同色の「L字型」（正方形の右上以外の頂点）を作りましょう。実はこれは何色で塗り分けても存在します。

f:id:fibonacci_freak:20170802121415p:plain

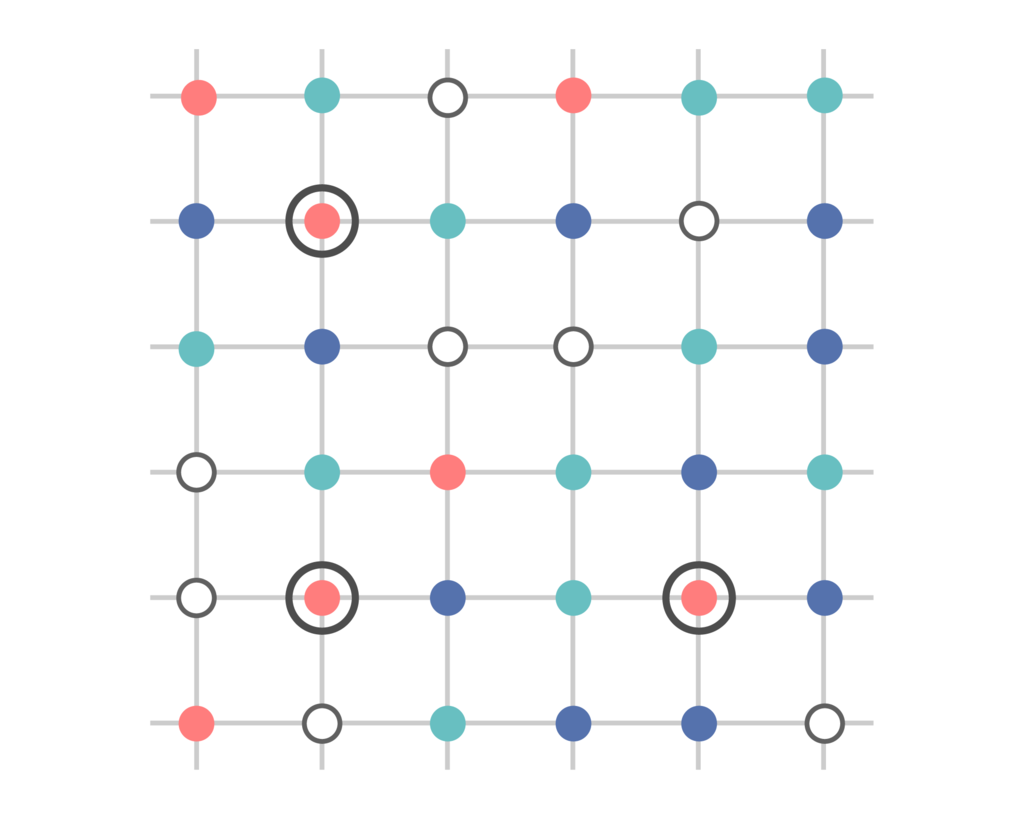
同色のL字型が無いと仮定します。すると実は十分大きい正方形領域をとれば、下図のような「左上の頂点を共有する $k-1$ 個のL字型の集まりで、各段の色が異なるもの」を見つけることができるのです。このような点の集まりををわかりやすく「 $k$ 段のオブジェ」と呼び、左上の頂点をその先端と呼ぶことにしましょう。

f:id:fibonacci_freak:20170802122808p:plain

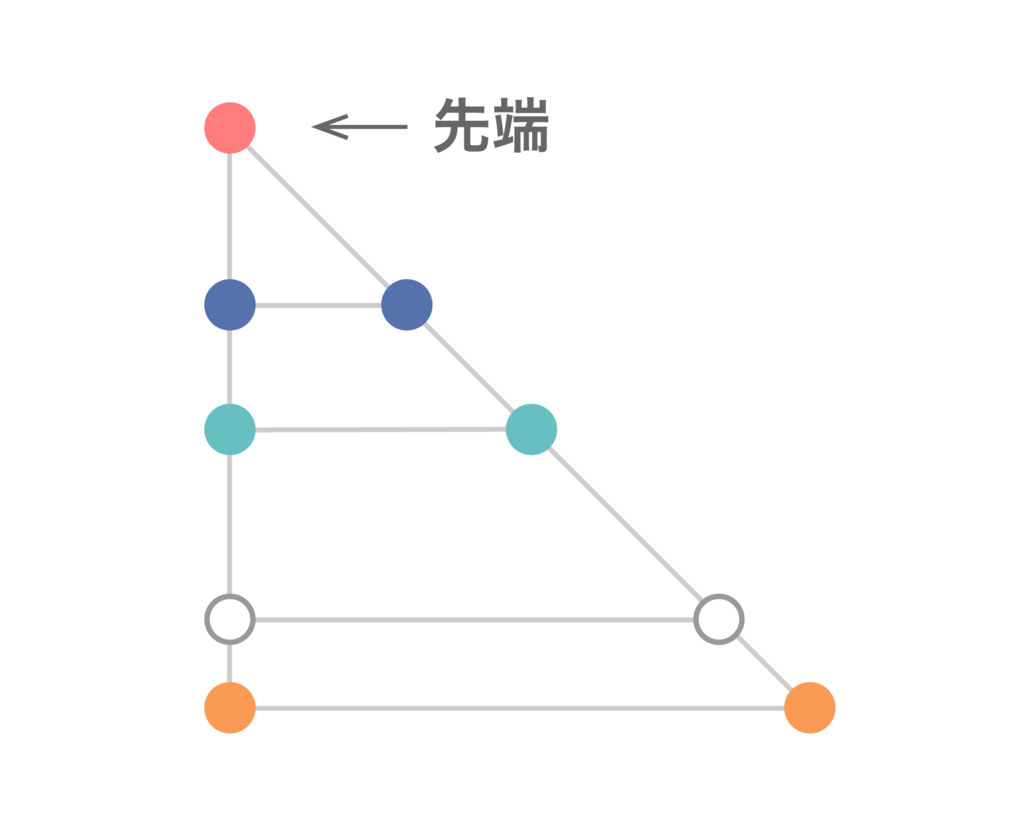
さて、実際に $k$ 段のオブジェを見つける方法を帰納的に示します。 $k=1$ のときは任意に1点とればそれが $1$ 段のオブジェになります。 $k\gt 1$ のとき、帰納法の仮定によりある整数 $N$ について $N\times N$ の正方形領域をとれば必ずその中に $k-1$ 段のオブジェが存在します。そこで $N\times N$ の正方形の列を $x$ 軸に平行にとり、それぞれの正方形に含まれる $k-1$ 段のオブジェを1つずつ選びます。そしてこれらの正方形に「選んだオブジェの配色と配置」を記したラベルをつけます。するとラベルの種類は有限なので、同じラベルのついた2つの正方形を取ることができます。

f:id:fibonacci_freak:20170802124137p:plain

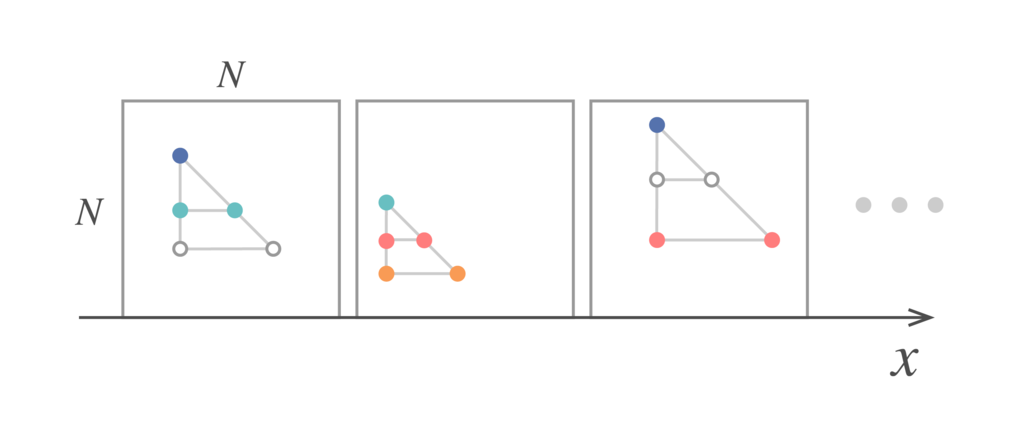
これで同じ配色の $k-1$ 段のオブジェが横に2つ並んだ状況ができました。このときオブジェの先端2つとL字型をなす点 $P$ をとると、 $P$ はオブジェの各段の点ともL字型をなしているので、「同色のL字型が無い」という仮定よりオブジェに含まれるどの色とも異なる色で塗られていなければなりません。よって $P$ と2つのオブジェを合わせれば $k$ 段のオブジェができます。

f:id:fibonacci_freak:20170802124934p:plain

このように任意の段数のオブジェを作ることができるのですが、使う色は有限種類なのでそれより多い段数のオブジェを作ることはできず、矛盾します。これで同色のL字型が存在することが示せました！

2色の場合に戻りましょう。L字型が取れれば、正方形を見つけるのは簡単です。上に書いたことよりある整数 $M$ について、 $M\times M$ の正方形領域には必ず同色のL字型があります。そこで平面を $M\times M$ の正方形たちに分割し、各々に含まれる同色のL字型を1つずつ選んで、その色と配置を記したラベルをつけます。正方形たちを格子点とみなしラベルを色とみなすと、再び上に書いたことより、L字型に並んだ同じラベルの正方形3つを見つけることができます。このとき各正方形内のL字型を集めれば、下図左のように全て同色のL字型がL字型に並んだものが得られます。わかりやすいように、これらL字型の色を青, もう片方の色を赤とします。

f:id:fibonacci_freak:20170802130606p:plain

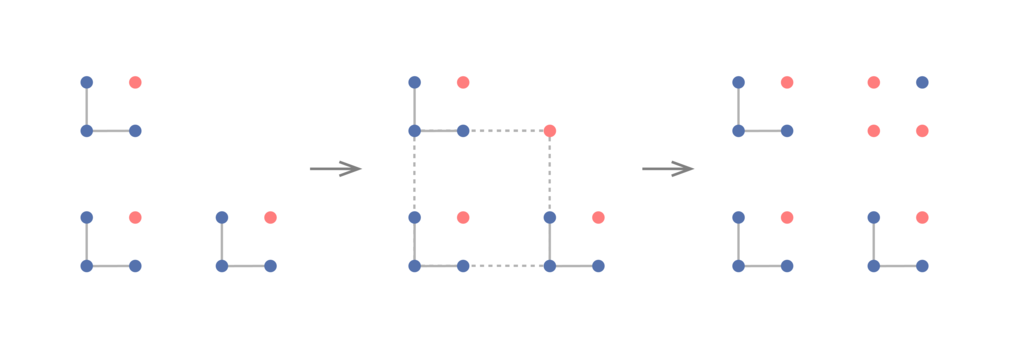
同色の正方形が存在しないとすると、小さいL字型の右上は赤となります（左）。また破線の正方形の右上の頂点も赤でなくてはいけません（中）。同じように右上の4点の色が定まります（右）。このとき一番外側の正方形は全て青で塗られており矛盾します。よって同色の正方形が存在することが示されました。

フィボナッチ・フリーク

数学の小ネタ集。

HEXは先手必勝である

HEXの定理(2)

HEXの定理(1)

痩せた集合・太った集合

自作数学パズル保管所を開設しました

素数の無限性の一風変わった証明

格子点を2色で塗り分ける問題